Lie Groups and Lie Algebras Lecture 2 notes
Definition: Manifold
A (topological) manifold of dimension is a topological space s.t. each point admits a neighborhood homeomorphic to an open subset
i.e. is locally -dimensionally euclidian.
, together with a homeomorphism is called a chart. A collection of charts covering is called an atlas.
Fixing a chart is equivalent to defining local coordinates on , with .
We also assume the following conditions:
- is hausdorff, i.e. you can distinguish any two points, i.e. any two distinct points have disjoint neighborhoods.
- admits a countable atlas
Smooth: of class (i.e. infinitely differentiable)
We want smooth manifolds because we want to work with local coordinates in our manifold like we may in . The problem is if some points belong to several charts, we have several choices for local coordinates and we want them to match/correspond.
A manifold is smooth if the transition functions between any two local coordinate systems are smooth.
That is, given two coordinate maps and , the transition function , which takes points in to points in , should be smooth.
If is smooth, then the transition functions should be smooth.
Examples of manifolds:
- Vector space
- Any open set of
- Graph of a smooth function (map)
- Two dimensional surfaces
- Spheres and projective spaces
- Lie Groups (of course)
- Homogeneous spaces of Lie groups
- Subsets in given by a system of equations (with certain "regularity" conditions, guaranteed by implicit function theorem)
Theorem: Implicit Function Theorem
In , consider a system of equations where are smooth and . Let be the set of solutions.
Then, the rank of the jacobi matrix is maximal (that is, ) at any point .
In other words, because we can think of each row of the matrix as a vector, and because we know that it must be linearly independent, we know that each system of equations must be linearly independent
Theorem: If the regularity condition holds, then carries the natural structure of a smooth manifold of dimension .
Example:
Consider the group as a subset in (3x3 matrices). The condition is a matrix equation which is equivalent to a system of 6 usual equations:
Then, if we find the jacobi matrix, we see that it's a block-triangular matrix. We see that if we add the ranks of each block, we get 6, so the matrix has rank 6. Therefore, is a dimensional smooth manifold.
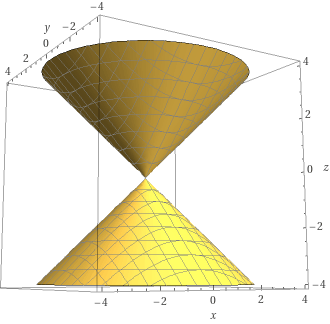
Another example:
Consider , a cone, in given by .
At most points, the regularity condition holds. But at , the derivative is so the condition fails and , as a whole, is not a smooth manifold.
Looking at itself, it's easy to see that isn't smooth because doesn't have a neighborhood homeomorphic to a -disk.
A continuous map between smooth manifolds is smooth if it is so in local coordinates.
More precisely, if and its image, with coordinates and in neighborhoods of and resp, then can be written using these local coordinates:
, i.e.
Smoothness of means that all are smooth.
Since the transition functions between charts are smooth, the above definition does not depend on the choice of local coordinates.
Definition: Diffeomorphism
A diffeomorphism is a smooth bijective map such that its inverse is also smooth. #-> So basically an isomorphism in the context of manifolds
Tangent Vectors
In the simple sense, if we have a manifold embedded in , a tangent vector at a point is just a tangent vector to a smooth curve passing through .
The set of all vectors at is the tangent space to at .
If we let be a smooth curve in , i.e. a smooth map from , then in local coordinates .
Then, the tangent vector to gamma at point is defined to be simply
So, in local coordinates, any tangent vector is given as an -tuple.
The problem is when we change local coordinate systems, as our function will be defined by new functions. Then, the new tangent vector in the new coordinates becomes
Then, if the original tangent vector is , then the same vector in the new coordinate system becomes
Definition: Tangent Vector
A tangent vector at point is defined in any local coordinate system as an -tuple.
In addition, it is required that the transformation law for the components of is given by the above equation.